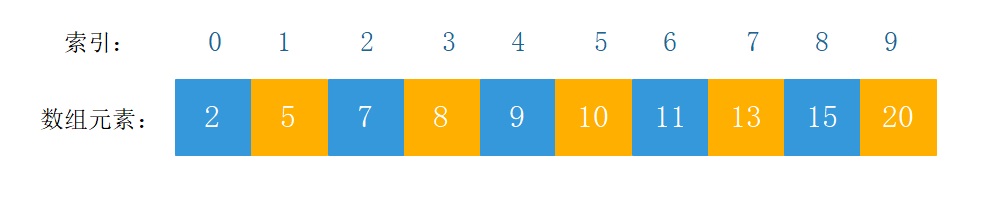
顺序表，线性表的一种，其存储时需要开辟一块足够大的连续的空间，数据之间的存放是相连的，中间没有空隙。

顺序表的初始化：需要指定顺序表的大小，这个大小要足够大，还要将元素个数初始化为0。

按照位置查找元素：可以查找指定位置的元素，这个通过下标可以快速找到。常数时间复杂度。

查找指定元素的位置：给定一个元素，查找其所在的位置。这个可以从第一个元素开始，遍历所有元素进行查找，找到第一个后就可以返回。

插入元素：在指定位置插入元素。首先位置是要合法的，这个可以进行判断；在插入时，首先需要从最后一个元素开始，一直到插入位置的元素将它们向后移动一个位置。移动完毕后将要插入的元素写入到对应位置。当然元素个数也要相应的加一。

注：以上两图来自于LeetCode，链接：https://leetcode-cn.com/leetbook/read/array-and-string/yjcir/

删除元素：比插入要简单一点，直接将要删除元素后的元素向前移动一个位置就可以。元素个数要相应的减一。插入和删除要素要大量的进行元素的移动操作，这严重影响了顺序表的效率。

注：上图来自于LeetCode，链接：https://leetcode-cn.com/leetbook/read/array-and-string/yjcir/

以下代码根据某课程进行了少量的修改，有问题还请理解。

/*
线性表的顺序存储结构，数据在内存中是连续存储的，C语言中主要是通过数组来实现
其插入删除操作时，由于要进行大量的数据移动操作，涉及到大量的数据拷贝等工作，
所以效率比较低。以下代码实现了线性表顺序存储结构的初始化、查找、插入、删除等操作。
*/
#include <stdio.h>
#include <stdlib.h>

#define LIST_INIT_SIZE 100
#define LIST_INCREAMENT 10

typedef int ElemTYPE;

//顺序表的结构，包括数据，长度，表的大小
typedef struct SqList
{
    ElemTYPE *elem;
    int length;
    int list_size;
} SqList, *Ptr;

typedef Ptr SqListPtr;

//状态
typedef enum Status
{
    success,
    fail,
    range_error
} Status;

Status List_Init(SqListPtr L);                              //线性表顺序存储结构初始化生成一个空表
Status List_Retrivsl(SqListPtr L, int pos, ElemTYPE *elem); //按位置查找
Status List_Locate(SqListPtr L, ElemTYPE elem, int *pos);   //按值查找位置
Status List_Insert(SqListPtr L, int pos, ElemTYPE elem);    //插入元素
Status List_Delete(SqListPtr L, int pos);                   //删除元素
void print_data(SqListPtr L);                               //打印数据

int main()
{
    SqListPtr list;
    printf("initial data
");
    List_Init(list);
    printf("insert 5 data:
");
    ElemTYPE data;
    for (int i = 1; i < 6; i++)
    {
        scanf("%d", &data);
        List_Insert(list, i, data);
    }
    print_data(list);

    printf("
");
    printf("delete data:
");
    int pos;
    scanf("%d", &pos);
    List_Delete(list, pos);
    print_data(list);
    printf("
");

    ElemTYPE elem;

    printf("the position you will find:
");
    scanf("%d", &pos);
    List_Retrivsl(list, pos, &elem);
    printf("%d
", elem);

    printf("the element you will find:
");
    scanf("%d", &elem);
    List_Locate(list,elem,&pos);
    printf("%d
",pos);

    system("pause");
    return 0;
}

Status List_Init(SqListPtr L)
{
    Status s = success;
    L->list_size = LIST_INIT_SIZE;
    L->length = 0;
    L->elem = (ElemTYPE *)malloc(sizeof(ElemTYPE) * L->list_size);
    if (L->elem == NULL)
    {
        s = fail;
    }
    return s;
}

Status List_Retrivsl(SqListPtr L, int pos, ElemTYPE *elem)
{
    Status s = range_error;
    if (L)
    {
        if ((pos - 1) >= 0 && (pos - 1) < L->length)
        {
            *elem = L->elem[pos - 1];
            s = success;
        }
    }
    return s;
}

Status List_Locate(SqListPtr L, ElemTYPE elem, int *pos)
{
    Status s = range_error;
    if (L)
    {
        for (int i = 0; i < L->length; ++i)
        {
            if (L->elem[i] == elem)
            {
                *pos = i + 1;
                s = success;
                break;
            }
        }
    }
    else
    {
        s = fail;
    }
    return s;
}

Status List_Insert(SqListPtr L, int pos, ElemTYPE elem)
{
    Status s = range_error;
    if ((pos - 1) >= 0 && (pos - 1) <= L->length)
    {
        for (int i = L->length - 1; i >= pos - 1; --i)
        {
            L->elem[i + 1] = L->elem[i];
        }
        L->elem[pos - 1] = elem;
        L->length++;
        s = success;
    }
    else
    {
        s = fail;
    }

    return s;
}

Status List_Delete(SqListPtr L, int pos)
{
    Status s = range_error;
    if ((pos - 1) >= 0 && (pos - 1) <= L->length)
    {

        if (L && L->length > 0)
        {
            for (int i = pos; i < L->length; ++i)
            {
                L->elem[i - 1] = L->elem[i];
            }
            L->length--;
            s = success;
        }
    }
    else
    {
        s = fail;
    }
    return s;
}

void print_data(SqListPtr L)
{
    for (int i = 0; i < L->length; i++)
    {
        printf("%d ", L->elem[i]);
    }
}